Связность объектов
В классическом методе Л. Констентайна и Э. Йордана определены семь типов связности.
1. Связность по совпадению. В модуле отсутствуют явно выраженные внутренние связи.
2. Логическая связность. Части модуля объединены по принципу функционального подобия.
3. Временная связность. Части модуля не связаны, но необходимы в один и тот же период работы системы.
4. Процедурная связность. Части модуля связаны порядком выполняемых ими действий, реализующих некоторый сценарий поведения.
5. Коммуникативная связность. Части модуля связаны по данным (работают с одной и той же структурой данных).
6. Информационная (последовательная) связность. Выходные данные одной части используются как входные данные в другой части модуля.
7. Функциональная связность. Части модуля вместе реализуют одну функцию.
Этот метод функционален по своей природе, поэтому наибольшей связностью здесь объявлена функциональная связность. Вместе с тем одним из принципиальных преимуществ объектно-ориентированного подхода является естественная связанность объектов.
Максимально связанным является объект, в котором представляется единая сущность и в который включены все операции над этой сущностью. Например, максимально связанным является объект, представляющий таблицу символов компилятора, если в него включены все функции, такие как «Добавить символ», «Поиск в таблице» и т. д.
Следовательно, восьмой тип связности можно определить так:
8. Объектная связность. Каждая операция обеспечивает функциональность, которая предусматривает, что все свойства объекта будут модифицироваться, отображаться и использоваться как базис для предоставления услуг.
Высокая связность — желательная характеристика, так как она означает, что объект представляет единую часть в проблемной области, существует в едином пространстве.
При изменении системы все действия над частью инкапсулируются в едином компоненте. Поэтому для производства изменения нет нужды модифицировать много компонентов.
Если функциональность в объектно-ориентированной системе обеспечивается наследованием от суперклассов, то связность объекта, который наследует свойства и операции, уменьшается. В этом случае нельзя рассматривать объект как отдельный модуль — должны учитываться все его суперклассы. Системные средства просмотра содействуют такому учету. Однако понимание элемента, который наследует свойства от нескольких суперклассов, резко усложняется.
Обсудим конкретные метрики для вычисления связности классов.
Метрики связности по данным
Л. Отт и Б. Мехра разработали модель секционирования класса [55]. Секционирование основывается на экземплярных переменных класса. Для каждого метода класса получают ряд секций, а затем производят объединение всех секций класса. Измерение связности основывается на количестве лексем данных (data tokens), которые появляются в нескольких секциях и «склеивают» секции в модуль. Под лексемами данных здесь понимают определения констант и переменных или ссылки на константы и переменные.
Базовым понятием методики является секция данных. Она составляется для каждого выходного параметра метода. Секция данных — это последовательность лексем данных в операторах, которые требуются для вычисления этого параметра.
Например, на рис. 14.1 представлен программный текст метода SumAndProduct. Все лексемы, входящие в секцию переменной SumN, выделены рамками. Сама секция для SumN записывается как следующая последовательность лексем:
N1 • SumN1
• I1 • SumN2 • O1 • I2 • 12
• N2 • SumN3 SumN4 • I3.
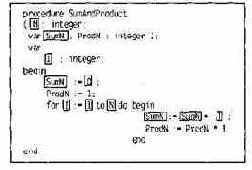
Рис. 14.1. Секция данных для переменной SumN
Заметим, что индекс в «12» указывает на второе вхождение лексемы «1» в текст метода. Аналогичным образом определяется секция для переменной ProdN:
N1 • ProdN1 • I1 • ProdN2 •11 • I2 • 12 • N2 • ProdN3 • ProdN4 • I4
Для определения отношений между секциями данных можно показать профиль секций данных в методе.
Для нашего примера профиль секций данных приведен в табл. 14.1.
Таблица 14.1. Профиль секций данных для метода SumAndProduct
|
SumN |
ProdN |
Оператор |
|
|
|
procedure SumAndProduct |
|
1 |
1 |
(Niinteger; |
|
1 |
1 |
varSumN, ProdNiinteger) |
|
|
|
var |
|
1 |
1 |
l:integer; |
|
|
|
begin |
|
2 |
|
SumN:=0 |
|
|
2 |
ProdN:=1 |
|
3 |
3 |
for l:=1 to N do begin |
|
3 |
|
SumN:=SumN+l |
|
|
3 |
ProdN:=ProdN*l |
|
|
|
end |
|
|
|
end; |
Еще одно базовое понятие методики — секционированная абстракция. Секционированная абстракция — это объединение всех секций данных метода. Например, секционированная абстракция метода SumAndProduct имеет вид
SA(SumAndProduct) = {N1
• SumN1 • I1 • SumN2 • 01 • I2 • I2 • N2
• SumN3 • SumN4 • I3,
N1
• ProdN1 • I1 • ProdN2
• I1 • I2 • I2 • N2
• ProdN3 • ProdN4 • I4}.
Введем главные определения.
Секционированной абстракцией класса (Class Slice Abstraction) CSA(C) называют объединение секций всех экземплярных переменных класса. Полный набор секций составляют путем обработки всех методов класса.
Склеенными лексемами называют те лексемы данных, которые являются элементами более чем одной секции данных.
Сильно склеенными лексемами называют те склеенные лексемы, которые являются элементами всех секций данных.
Сильная связность по данным (StrongData Cohesion) — это метрика, основанная на количестве лексем данных, входящих во все секции данных для класса. Иначе говоря, сильная связность по данным учитывает количество сильно склеенных лексем в классе С, она вычисляется по формуле:

где SG(CSA(C)) — объединение сильно склеенных лексем каждого из методов класса С, лексемы(С) — множество всех лексем данных класса С.
Таким образом, класс без сильно склеенных лексем имеет нулевую сильную связность по данным.
Слабая связность по данным (Weak Data Cohesion) — метрика, которая оценивает связность, базируясь на склеенных лексемах.
Склеенные лексемы не требуют связывания всех секций данных, поэтому данная метрика определяет более слабый тип связности. Слабая связность по данным вычисляется по формуле:

где G(CSA(C)) — объединение склеенных лексем каждого из методов класса. Класс без склеенных лексем не имеет слабой связности по данным. Наиболее точной метрикой связности между секциями данных является клейкость данных (Data Adhesiveness). Клейкость данных определяется как отношение суммы из количеств секций, содержащих каждую склеенную лексему, к произведению количества лексем данных в классе на количество секций данных. Метрика вычисляется по формуле:

Приведем пример. Применим метрики к классу, профиль секций которого показан в табл. 14.2.
Таблица 14.2. Профиль секций данных для класса Stack
|
array top size |
Класс Stack |
|
|
class Stack {int *array, top, size; |
|
|
public: |
|
|
Stack (int s) { |
|
2 2 |
size=s; |
|
2 2 |
array=new int [size]; |
|
2 |
top=0;} |
|
|
int IsEmpty () { |
|
2 |
return top==0}; |
|
|
int Size (){ |
|
2 |
return size}; |
|
|
intVtop(){ |
|
3 3 |
return array [top-1]; } |
|
|
void Push (int item) { |
|
2 2 2 |
if (top= =size) |
|
|
printf ("Empty stack. \n"); |
|
|
else |
|
3 3 3 |
array [top++]=item;} |
|
|
int Pop () { |
|
1 |
if (IsEmpty ()) |
|
|
printf ("Full stack. \n"); |
|
|
else |
|
1 |
--top;} |
|
|
}; |
Расчеты по рассмотренным метрикам дают следующие значения:
SDC(CSA(Stack)) = 5/19 = 0,26
WDC(CSA(Stack)) = 12/19 = 0,63
DA(CSA(Stack)) =(7*2 + 5*3)/(19*3) = 0,51
Метрики связности по методам
Д. Биемен и Б. Кенг предложили метрики связности класса, которые основаны на прямых и косвенных соединениях между парами методов [15]. Если существуют общие экземплярные переменные (одна или несколько), используемые в паре методов, то говорят, что эти методы соединены прямо.
Пара методов может быть соединена косвенно, через другие прямо соединенные методы.
На рис. 14.2 представлены отношения между элементами класса Stack. Прямоугольниками обозначены методы класса, а овалами — экземплярные переменные. Связи показывают отношения использования между методами и переменными.
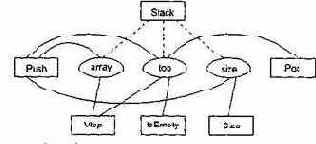
Рис. 14. 2. Отношения между элементами класса Stack
Из рисунка видно, что экземплярная переменная top используется методами Stack, Push, Pop, Vtop и IsEmpty. Таким образом, все эти методы попарно прямо соединены. Напротив, методы Size и Pop соединены косвенно: Size соединен прямо с Push, который, в свою очередь, прямо соединен с Pop. Метод Stack является конструктором класса, то есть функцией инициализации. Обычно конструктору доступны все экземплярные переменные класса, он использует эти переменные совместно со всеми другими методами. Следовательно, конструкторы создают соединения и между такими методами, которые никак не связаны друг с другом. Поэтому ни конструкторы, ни деструкторы здесь не учитываются. Связи между конструктором и экземплярными переменными на рис. 14.2 показаны пунктирными линиями.
Для формализации модели вводятся понятия абстрактного метода и абстрактного класса.
Абстрактный метод АМ(М) — это представление реального метода М в
виде множества экземплярных переменных, которые прямо или косвенно используются методом.
Экземплярная переменная прямо используется методом М, если она появляется в методе как лексема данных. Экземплярная переменная может быть определена в том же классе, что и М, или же в родительском классе этого класса. Множество экземплярных переменных, прямо используемых методом М, обозначим как DU(M).
Экземплярная переменная косвенно используется методом М, если: 1) экземплярная переменная прямо используется другим методом М', который вызывается (прямо или косвенно) из метода М; 2) экземплярная переменная, прямо используемая методом М', находится в том же объекте, что и М.
Множество экземплярных переменных, косвенно используемых методом М, обозначим как IU(М).
Количественно абстрактный метод формируется по выражению:
AM (М) = DU (М)

Абстрактный класс АС(С) — это представление реального класса С в виде совокупности абстрактных методов, причем каждый абстрактный метод соответствует видимому методу класса С. Количественно абстрактный класс формируется по выражению:
АС (С) = [[AM (M) | M

где V(C) — множество всех видимых методов в классе С
и в классах — предках для С.
Отметим, что АМ-представления различных методов могут совпадать, поэтому в АС могут быть дублированные элементы. В силу этого АС записывается в форме мультимножества (двойные квадратные скобки рассматриваются как его обозначение).
Локальный абстрактный класс LAC(C) — это совокупность абстрактных методов, где каждый абстрактный метод соответствует видимому методу, определенному только внутри класса С. Количественно абстрактный класс формируется по выражению:
LAC(C)=[[AM(M)|M

где LV(C) — множество всех видимых методов, определенных в классе С.
Абстрактный класс для стека, приведенного в табл. 14.2, имеет вид:
AC (Stack) = [[{top}, {size}, {array, top}, {array, top, size}, {pop}]].
Поскольку класс Stack не имеет суперкласса, то справедливо:
AC (Stack) = LAC (Stack)
Пусть NP(C) — общее количество пар абстрактных методов в AC(C). NP определяет максимально возможное количество прямых или косвенных соединений в классе. Если в классе С имеются N методов, тогда NP(C) = N*(N- l)/2. Обозначим:
q NDC(C) — количество прямых соединений AC(Q;
q NIC(C) — количество косвенных соединений в АС(С).
Тогда метрики связности класса можно представить в следующем виде:
q сильная связность класса (Tight Class Cohesion (ТСС)) определяется относительным количеством прямо соединенных методов:
ТСС (С) = NDC (С) / NP (С);
q слабая связность класса (Loose Class Cohesion (LCC)) определяется относительным количеством прямо или косвенно соединенных методов:
LCC (С) = (NDC (С) + NIC (С)) / NP (С).
Очевидно, что всегда справедливо следующее неравенство:
LCC(C)>=TCC(C).
Для класса Stack метрики связности имеют следующие значения:
TCC(Stack)=7/10=0,7
LCC(Stack)=10/10=l
Метрика ТСС показывает, что 70% видимых методов класса Stack соединены прямо, а метрика LCC показывает, что все видимые методы класса Stack соединены прямо или косвенно.
Метрики ТСС и LCC индицируют степень связанности между видимыми методами класса. Видимые методы либо определены в классе, либо унаследованы им. Конечно, очень полезны метрики связности для видимых методов, которые определены только внутри класса — ведь здесь исключается влияние связности суперкласса. Очевидно, что метрики локальной связности класса определяются на основе локального абстрактного класса. Отметим, что для локальной связности экземплярные переменные и вызываемые методы могут включать унаследованные переменные.
