Способ диаграмм причин-следствий
Диаграммы причинно-следственных связей — способ проектирования тестовых вариантов, который обеспечивает формальную запись логических условий и соответствующих действий [3], [64]. Используется автоматный подход к решению задачи.
Шаги способа:
1) для каждого модуля перечисляются причины (условия ввода или классы эквивалентности условий ввода) и следствия (действия или условия вывода). Каждой причине и следствию присваивается свой идентификатор;
2) разрабатывается граф причинно-следственных связей;
3) граф преобразуется в таблицу решений;
4) столбцы таблицы решений преобразуются в тестовые варианты.
Изобразим базовые символы для записи графов причин и следствий (cause-effect graphs).
Сделаем предварительные замечания:
1) причины будем обозначать символами сi, а следствия — символами еi;
2) каждый узел графа может находиться в состоянии 0 или 1 (0 — состояние отсутствует, 1 — состояние присутствует).
Функция тождество (рис. 7.4) устанавливает, что если значение с1 есть 1, то и значение е1
есть 1; в противном случае значение е1 есть 0.

Рис. 7.4. Функция тождество
Функция не (рис. 7.5) устанавливает, что если значение с1 есть 1, то значение e1 есть 0; в противном случае значение е1
есть 1.

Рис. 7.5. Функция не
Функция или (рис. 7.6) устанавливает, что если с1 или с2 есть 1, то е1 есть 1, в противном случае e1 есть 0.
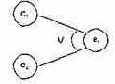
Рис. 7.6. Функция или
Функция и (рис. 7.7) устанавливает, что если и с1 и с2 есть 1, то е1
есть 1, в противном случае е1 есть 0.
Часто определенные комбинации причин невозможны из-за синтаксических или внешних ограничений. Используются перечисленные ниже обозначения ограничений.
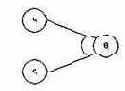
Рис. 7.7. Функция и
Ограничение Е (исключает, Exclusive, рис. 7.8) устанавливает, что Е должно быть истинным, если хотя бы одна из причин — а или b — принимает значение 1 (а и b не могут принимать значение 1 одновременно).
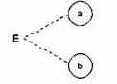
Рис. 7.8. Ограничение Е (исключает, Exclusive)
Ограничение I (включает, Inclusive, рис. 7.9) устанавливает, что по крайней мере одна из величин, а, b, или с, всегда должна быть равной 1 (а, b и с не могут принимать значение 0 одновременно).
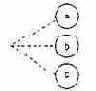
Рис. 7.9. Ограничение I (включает, Inclusive)
Ограничение О (одно и только одно, Only one, рис. 7.10) устанавливает, что одна и только одна из величин а или b должна быть равна 1.
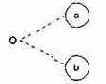
Рис. 7.10. Ограничение О (одно и только одно, Only one)
Ограничение R (требует, Requires, рис. 7.11) устанавливает, что если а принимает значение 1, то и b должна принимать значение 1 (нельзя, чтобы а было равно 1, a b - 0).
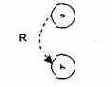
Рис. 7.11. Ограничение R (требует, Requires)
Часто возникает необходимость в ограничениях для следствий.
Ограничение М (скрывает, Masks, рис. 7.12) устанавливает, что если следствие а имеет значение 1, то следствие b должно принять значение 0.
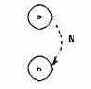
Рис. 7.12. Ограничение М (скрывает, Masks)
Для иллюстрации использования способа рассмотрим пример, когда программа выполняет расчет оплаты за электричество по среднему или переменному тарифу.
При расчете по среднему тарифу:
q при месячном потреблении энергии меньшем, чем 100 кВт/ч, выставляется фиксированная сумма;
q при потреблении энергии большем или равном 100 кВт/ч применяется процедура А планирования расчета.
При расчете по переменному тарифу:
q при месячном потреблении энергии меньшем, чем 100 кВт/ч, применяется процедура А планирования расчета;
q при потреблении энергии большем или равном 100 кВт/ч применяется процедура В планирования расчета.
Шаг 1. Причинами являются:
1) расчет по среднему тарифу;
2) расчет по переменному тарифу;
3) месячное потребление электроэнергии меньшее, чем 100 кВт/ч;
4) месячное потребление электроэнергии большее или равное 100 кВт/ч.
На основе различных комбинаций причин можно перечислить следующие следствия:
q 101 — минимальная месячная стоимость;
q 102 — процедура А планирования расчета;
q 103 — процедура В планирования расчета.
Шаг 2. Разработка графа причинно-следственных связей (рис. 7.13).
Узлы причин перечислим по вертикали у левого края рисунка, а узлы следствий — у правого края рисунка. Для следствия 102 возникает необходимость введения вторичных причин — 11 и 12, — их размещаем в центральной части рисунка.
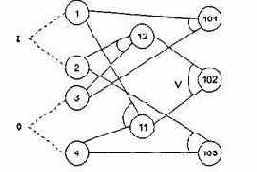
Рис. 7.13. Граф причинно-следственных связей
Шаг 3. Генерация таблицы решений. При генерации причины рассматриваются как условия, а следствия — как действия.
Порядок генерации.
1. Выбирается некоторое следствие, которое должно быть в состоянии «1».
2. Находятся все комбинации причин (с учетом ограничений), которые устанавливают это следствие в состояние «1». Для этого из следствия прокладывается обратная трасса через граф.
3. Для каждой комбинации причин, приводящих следствие в состояние «1», строится один столбец.
4. Для каждой комбинации причин доопределяются состояния всех других следствий. Они помещаются в тот же столбец таблицы решений.
5. Действия 1-4 повторяются для всех следствий графа.
Таблица решений для нашего примера показана в табл. 7.1.
Шаг 4. Преобразование каждого столбца таблицы в тестовый вариант. В нашем примере таких вариантов четыре.
Тестовый вариант 1 (столбец 1) ТВ1:
ИД: расчет по среднему тарифу; месячное потребление электроэнергии 75 кВт/ч.
ОЖ.РЕЗ.: минимальная месячная стоимость.
Тестовый вариант 2 (столбец 2) ТВ2:
ИД: расчет по переменному тарифу; месячное потребление электроэнергии 90 кВт/ч.
ОЖ.РЕЗ.: процедура A планирования расчета.
Тестовый вариант 3 (столбец 3) ТВЗ:
ИД: расчет по среднему тарифу; месячное потребление электроэнергии 100 кВт/ч.
ОЖ.РЕЗ.: процедура А планирования расчета.
Тестовый вариант 4 (столбец 4) ТВ4:
ИД: расчет по переменному тарифу; месячное потребление электроэнергии 100 кВт/ч.
ОЖ.РЕЗ.: процедура В планирования расчета.
Таблица 7.1. Таблица решений для расчета оплаты за электричество
|
Номера столбцов — > |
1 |
2 |
3 |
4 |
||
|
Условия |
Причины |
1 |
1 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
1 |
||
|
3 |
1 |
1 |
0 |
0 |
||
|
4 |
0 |
0 |
1 |
1 |
||
|
Вторичные причины |
11 |
0 |
0 |
1 |
0 |
|
|
12 |
0 |
1 |
0 |
0 |
||
|
Действия |
Следствия |
101 |
1 |
0 |
0 |
0 |
|
102 |
0 |
1 |
1 |
0 |
||
|
103 |
0 |
0 |
0 |
1 |
