Характеристики иерархической структуры программной системы
Иерархическая структура программной системы — основной результат предварительного проектирования. Она определяет состав модулей ПС и управляющие отношения между модулями. В этой структуре модуль более высокого уровня (начальник) управляет модулем нижнего уровня (подчиненным).
Иерархическая структура не отражает процедурные особенности программной системы, то есть последовательность операций, их повторение, ветвления и т. д. Рассмотрим основные характеристики иерархической структуры, представленной на рис. 4.17.
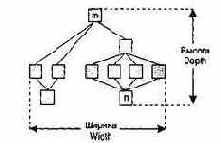
Рис. 4.17. Иерархическая структура программной системы
Первичными характеристиками являются количество вершин (модулей) и количество ребер (связей между модулями). К ним добавляются две глобальные характеристики — высота и ширина:
q высота — количество уровней управления;
q ширина — максимальное из количеств модулей, размещенных на уровнях управления.
В нашем примере высота = 4, ширина = 6.
Локальными характеристиками модулей структуры являются коэффициент объединения по входу и коэффициент разветвления по выходу.
Коэффициент объединения по входу Fan_in(i) — это количество модулей, которые прямо управляют i-м модулем.
В примере для модуля n: Fan_in(n)=4.
Коэффициент разветвления по выходу Fan_out(i) — это количество модулей, которыми прямо управляет i-й модуль.
В примере для модуля m: Fan_out(m)=3.
Возникает вопрос: как оценить качество структуры? Из практики проектирования известно, что лучшее решение обеспечивается иерархической структурой в виде дерева.
Степень отличия реальной проектной структуры от дерева характеризуется невязкой структуры. Как определить невязку?
Вспомним, что полный граф (complete graph) с п вершинами имеет количество ребер
ес=n(n-1)/2,
а дерево (tree) с таким же количеством вершин — существенно меньшее количество ребер
et=n-l.
Тогда формулу невязки можно построить, сравнивая количество ребер полного графа, реального графа и дерева.
Для проектной структуры с п вершинами и е ребрами невязка определяется по выражению

Значение невязки лежит в диапазоне от 0 до 1. Если Nev = 0, то проектная структура является деревом, если Nev = 1, то проектная структура — полный граф.
Ясно, что невязка дает грубую оценку структуры. Для увеличения точности оценки следует применить характеристики связности и сцепления.
Хорошая структура должна иметь низкое сцепление и высокую связность.
Л. Констентайн и Э. Йордан (1979) предложили оценивать структуру с помощью коэффициентов Fan_in(i) и Fan_out(i) модулей [77].
Большое значение Fan_in(i) — свидетельство высокого сцепления, так как является мерой зависимости модуля. Большое значение Fan_out(i) говорит о высокой сложности вызывающего модуля. Причиной является то, что для координации подчиненных модулей требуется сложная логика управления.
Основной недостаток коэффициентов Fan_in(i) и Fan_out(i) состоит в игнорировании веса связи. Здесь рассматриваются только управляющие потоки (вызовы модулей). В то же время информационные потоки, нагружающие ребра структуры, могут существенно изменяться, поэтому нужна мера, которая учитывает не только количество ребер, но и количество информации, проходящей через них.
С. Генри и Д. Кафура (1981) ввели информационные коэффициенты ifan_in(i) и ifan_out(j) [35]. Они учитывают количество элементов и структур данных, из которых i-й модуль берет информацию и которые обновляются j-м модулем соответственно.
Информационные коэффициенты суммируются со структурными коэффициентами sfan_in(i) и sfan_out( j), которые учитывают только вызовы модулей.
В результате формируются полные значения коэффициентов:
Fan_in (i) = sfan_in (i) + ifan_in (i),
Fan_out (j) = sfan_out (j) + ifan_out (j).
На основе полных коэффициентов модулей вычисляется метрика общей сложности структуры:
S =

где length(i) — оценка размера i-го модуля (в виде LOC- или FP-оценки).
