Графы, деревья и сети
Для описания многих видов абстрактных данных в информатике вообще и в теории искусственного интеллекта, в частности, очень широко используется терминология, заимствованная из теории графов. Следующие определения приведены здесь для того, чтобы показать, как эти заимствованные термины трактуются при описании структурированных объектов, что несколько отличается от их трактовки в "родной" математической сфере.
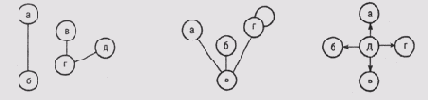
Рис. 6.1. Некоторые виды графов: а) обыкновенный граф; б) связный граф с петлей; в) обыкновенный ориентированный граф — дерево
Все определения сформулированы в предположении, что существуют два вида примитивов — узлы и связи. Узлы представляют собой исходящие и целевые пункты для связей и обычно каким-либо образом промаркированы. Связи также могут быть промаркированы, но это не обязательно. Все зависит от того, имеем ли мы дело со связями одного вида или разных. В общепринятой терминологии теории графов узлы называются "вершинами", а связи — "ребрами графа", или "дугами".
Определение 6.1. Если N— множество узлов, то любое подмножество NxN является обобщенным графом G. Если в парах подмножества NxN имеет значение порядок, то граф G является ориентированным.
На рис. 6.1 показаны разные типы графов. Обратите внимание на то, что граф не обязательно должен быть связным. Если задаться условием, что петли не допускаются, т.е. в каждой паре должны присутствовать разные узлы, то такой граф называется обыкновенным. Если на графе не допускаются не только петли, но и циклы (т.е. последовательность связей, в которой начальный и конечный узлы совпадают), то такой граф называется лесом.
Определение 6.2. Если G— обыкновенный граф, в котором имеется п узлов и п-1 связей и отсутствуют циклы, то такой граф является деревом.
Иными словами, дерево — это связный лес. Обычно один из узлов дерева является его корнем, например узел е на графе, представленном на рис. 6.1,в. Остальные узлы образуют ветвящуюся структуру "наследников" корневого узла, в которой отсутствуют циклы.
Узлы, не имеющие наследников, являются терминальными, или "листьями" дерева, а остальные узлы называются промежуточными (нетерминальными).
В теории графов сетью называется взвешенный ориентированный граф, т.е. граф, в котором каждой связи сопоставлено определенное число. Обычно этими числами оценивается "стоимость" пути вдоль этой связи или длина связи, как на карте дорог. В каждом конкретном случае применения графа как формального средства описания проблемы эти числа могут трактоваться по-своему.
Следующее определение сети более близко к специфике задач искусственного интеллекта, которыми мы сейчас занимаемся.
Определение 6.3. Если L — это множество взвешенных связей, a N, как и ранее, множество узлов, то сеть — это любое подмножество NxLxN, в котором имеет значение порядок в триадах.
Связи в сети практически всегда являются ориентированными, поскольку отношения, представленные взвешенными связями, не должны быть симметричными.
Обыкновенные графы используются для представления взаимоотношений между объектами в пространстве или во времени. Можно использовать их и для представления более абстрактных причинно-следственных связей, как, например, связей между различными видами патологий в медицине (рис. 6.2). Доступ к такой информации связан в той или иной мере с использованием специальных средств прослеживания путей на графе, для которых разработаны самые различные алгоритмы (см., например, работу [Pearl, 1984]).
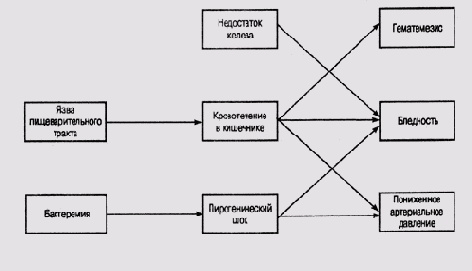
Рис. 6.2. Участок сети причинно-следственных связей ([Pople, 1982P
Для представления иерархических классификаций и сетей применяются деревья. Например, на рис. 6.3 показано дерево классификации болезней по расположению пораженного органа. Корневой узел дерева представляет множество всех болезней, а его наследники — группы болезней, соответствующие основному пораженному органу. Каждый из этих узлов будет иметь своих наследников, представляющих более узкие группы болезней, и т.д. Терминальные узлы дерева будут представлять конкретные заболевания.
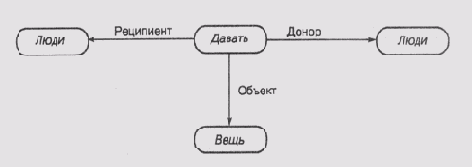
Семантические сети вначале использовались для представления смысла выражений естественного языка человека, откуда и появилось название этого класса сетей. Теперь же они используются в качестве структуры, пригодной для представления информации общего вида, — узлы представляют некоторые концепты (понятия), а связи — отношения между концептами. На рис. 6.4 представлены два фрагмента семантической сети. Первый фрагмент представляет глагол давать и показывает, что этот глагол может иметь три вида взаимодействия с остальными членами предложения: с донором, реципиентом и с объектом, который должен быть передан. Надписи в узлах, к которым подходят связи, соответствуют классу сущностей, которые могут выступать в качестве субъектов связи. Так, донор и реципиент, как правило, —люди, а то, что нужно передать, — вещь.
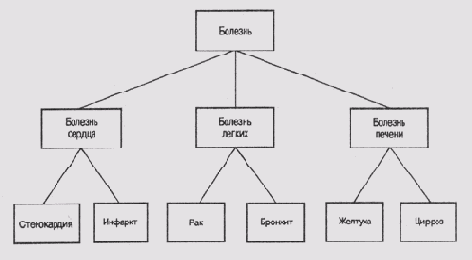
Рис. 6.3. Обыкновенное дерево классификации болезней
a
б
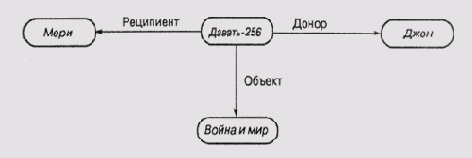
Рис. 6.4. Фрагменты семантической сети: а) представление глагола "давать "; б) представление конкретного действия
Второй фрагмент соответствует конкретной фразе или конкретной реализации действия, означенного этим глаголом. Эту реализацию мы назвали давать-265. Смысл фразы состоит в том, что Джон передает Мери книгу "Война и мир". Фразу можно считать допустимой, поскольку все ее члены удовлетворяют ограничениям, специфицированным соответствующими узлами сети. Джон и Мери принадлежат к классу люди, а "Война и мир" — к классу книга, который, в свою очередь, является одним из видов класса вещи.
Обычно узел давать-265 связывается с узлом давать связью, которая указывает, что давать-265 — это одна из конкретных реализаций концепта (в данном случае действия) давать. Такого рода специальные связи часто называют ISA-связями (связями типа "это есть...").
Термин ассоциативные сети лучше отражает характер использования такого рода формальных структур для тех задач, которые мы рассматриваем. Поскольку аппарат ассоциативных сетей все шире используется для моделирования объектов и их взаимосвязей в конкретных предметных областях, что необходимо для построения экспертных систем, ниже мы рассмотрим их более детально.
